Dr Alexei Blednykh of BNL had send us the Description of a Device
where he wants to know where the Energy lost by the Beam goes.
The Inputfile for this Device is
Inputfile
The Energy-Loss is the longitudinal Lossfactor.
A Wakepotential Computation gives a Energy Loss of
![]() Joules.
Joules.
gd1 < Inputfile | tee Logfile echo "-gen, inf @last, -wakes, shigh= 0.1, doit" | gd1.pp
A Plot of the longitudinal Wakepotential is shown in Figure 2.
The Lossfactor of
![]() Newton-Meter is indicated in the upper right Corner.
That Lossfactor as given by gd1.pp takes into Account the used two Planes of Symmetry.
Newton-Meter is indicated in the upper right Corner.
That Lossfactor as given by gd1.pp takes into Account the used two Planes of Symmetry.
The Energy in the considered Volume will leave through the Ports. We have a Look at the Signals at the Ports:
# Input for gd1.pp: -general, inf @last -spara, freq no, time yes, upto 3e-9, doitThree of the four resulting Plots are shown in Figures 3 through 5.
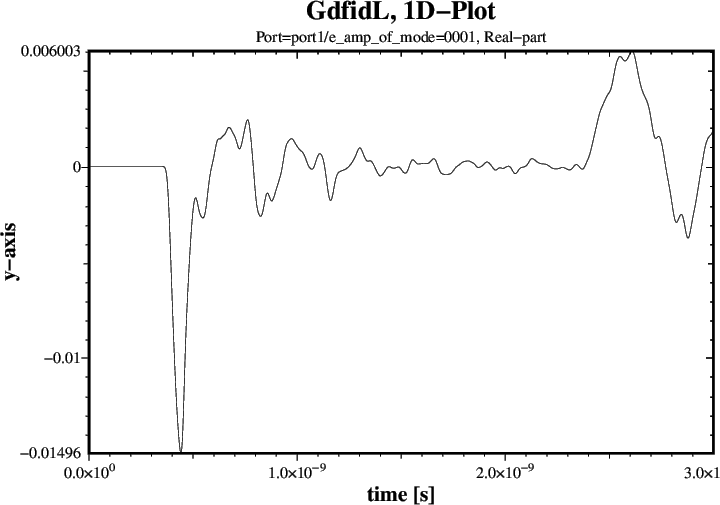 |
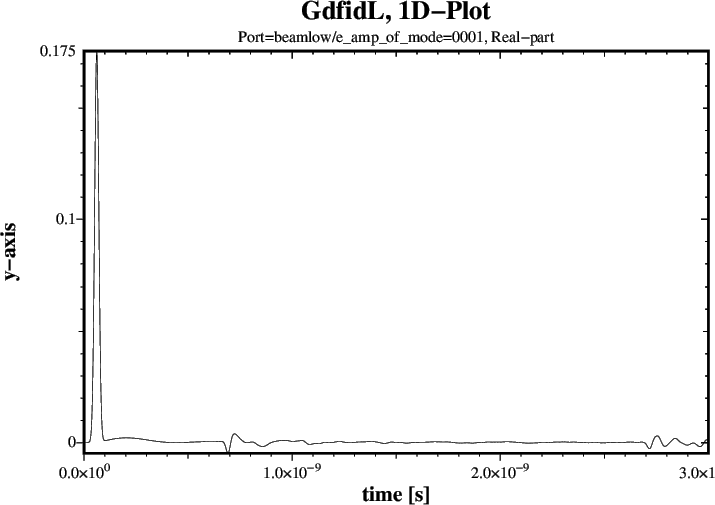 |
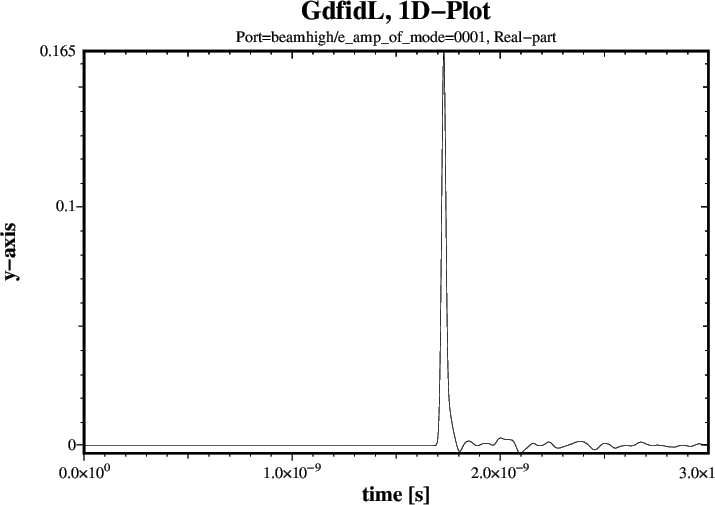 |
We compute the integrated Power Sum of all Modes:
# Input for gd1.pp:
-general, inf @last
-spara, freq no
time no, # time= yes, would give us Plots of all Signals.
modes= all, ports= all
tintpower= yes
upto 3e-9
doit
The resulting Plot is shown in Figure 6.
The reported Power up to t=3nS is 1.9
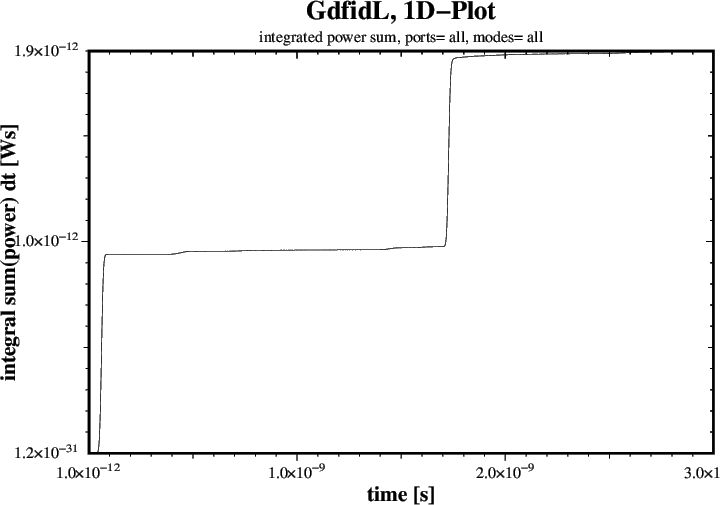 |
# Input for gd1.pp:
-general, inf @last
-spara, freq no
time no, # time= yes, would give us Plots of all Signals.
tintpower= yes
upto 3e-9
modes= all,
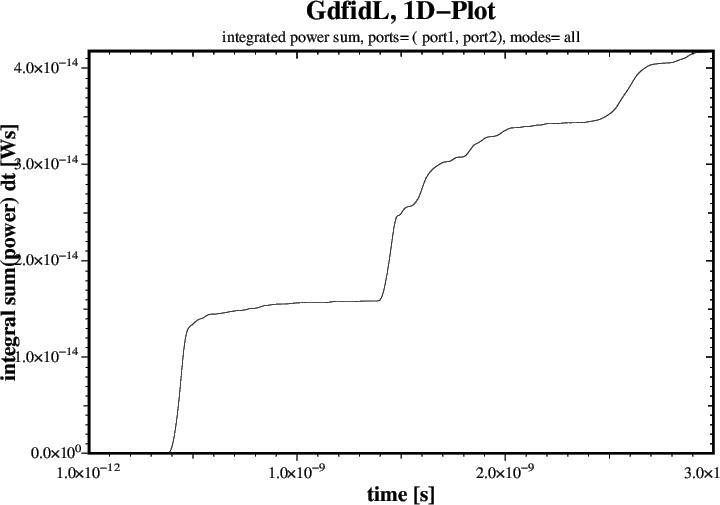
ports= ( port1, port2), doit # These Signals are not corrupted.
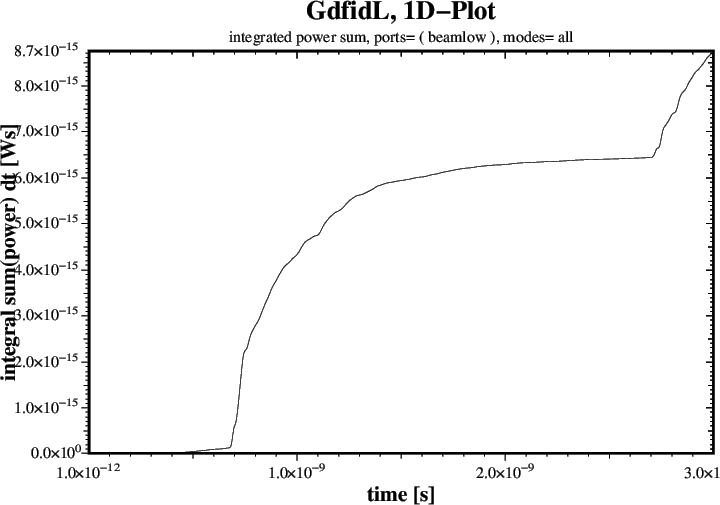
tfirst= 0.4e-9, ports= ( beamlow ), doit # Corrupted up to t= 2*0.35e-9
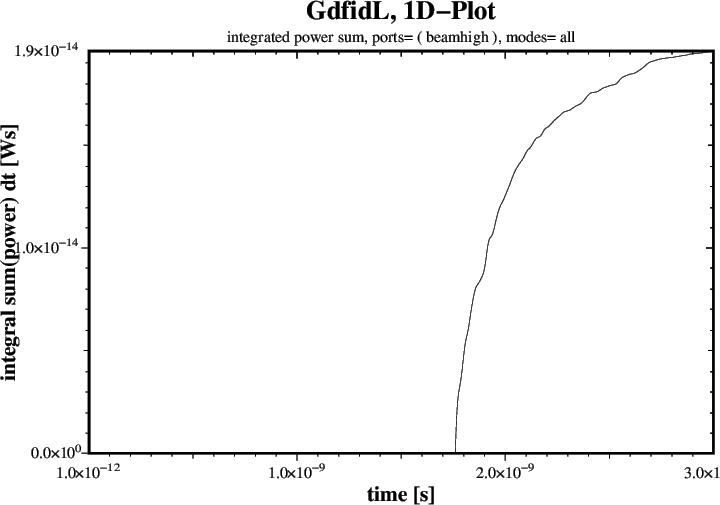
tfirst= 1.76e-9, ports= ( beamhigh ), doit # Corrupted up to t= 1.76e-9
The resulting Plots are shown in Figures 7 through 9.
 |
 |
 |
# Input for gd1.pp:
-general, inf @last
-energy
symbol= e_2, doit
symbol= h_2, doit
This gives:
############################################################################## # Flags: menu, prompt, message, # ############################################################################## # Section: -energy # ############################################################################## # symbol = h_2 # # quantity = h # # solution = 2 # # bbxlow = -1.0000e+30, bbylow = -1.0000e+30, bbzlow = -1.0000e+30 # # bbxhigh= 1.0000e+30, bbyhigh= 1.0000e+30, bbzhigh= 1.0000e+30 # # # # # # @henergy : 6.45617e-15 (symbol: h_2, m: 1) # # @eenergy : 8.02293e-15 (symbol: e_2, m: 1) # ############################################################################## # doit, ?, return, end, help, ls # ##############################################################################Our Energies so far:
6.45617e-15 # H-Energy at t=3e-9
8.02293e-15 # E-Energy at t=3e-9
42e-15 # Energy left through Port1 and Port2
8.7e-15 # Energy left through BeamLow
19.5e-15 # Energy left through BeamHigh
Sum: 84.7e-15 Joules