next_inactive up previous


How to perform computations with free moving charges

Computations with free moving charges are done by GdfidL using the Particle in Cell algorithm (PIC). The PIC computation normally consists of three steps.

Simplest form of PIC computation, initial fields are zero

The simplest form of a PIC computation is when the electromagnetic field at the time $t=0$ is zero, and there is no magnetostatic field. The needed steps for the PIC computation then are

The geometry

As geometry for this first simple case, we use an empty rectangular volume, with all walls electric walls. 
 define(STPSZE, 1/100)
 -mesh
    spacing= STPSZE           # The default grid spacing

    pxlow= -1/2, pxhigh= 1/2  # The borderplanes of the computational volume
    pylow= -1/2, pyhigh= 1/2  # pylow: Plane Y LOW
    pzlow= 0, pzhigh= 1

    cxlow= electric, cxhigh= electric # Condition at x=xlow, and at x=xhigh
    cylow= electric, cyhigh= electric
    czlow= electric, czhigh= electric
    
 #
 # Fill the 'universe' with vacuum:
 #
 -brick
    material= 0
       xlow= -INF, xhigh= INF
       ylow= -INF, yhigh= INF
       zlow= -INF, zhigh= INF
    doit

The free moving charges

The PIC algorithm is selected by specifying an external executable file which describes the properties of the free moving charges. 
 -fdtd
    -clouds
       #
       # We compile the executable file with the Fortran Compiler,
       #  (which is called 'fort' on this system)
       #
       system( fortran Eject-beam.f90 -o ./Eject-a.out )

       #
       # We specify that the properties of free moving charges
       # shall be described by the executable file 'Eject-a.out'
       #
       ejectioncommand=                    Eject-a.out
In addition, we have to specify the time which shall be simulated. And we should store some fields, to analyse the fields etc. 
 define(TMAX, 2/@clight)
 -fdtd
    -time
       tmin= TMAX
       tmax= TMAX

    -storefieldsat
       name= bla
          what= both   # 'what' could be 'e', 'b' or 'both'
                       # Clouds are stored anyway
          firstsaved= 0.1 / @clight
          lastsaved=    2 / @clight
          distance=   0.1 / @clight
       doit # do not forget this.

Now we can start the computation. 

 #
 # Start of computation:
 #
 -fdtd
     doit

The inputfile for this cavity is empty.gdf The sourcecode for the program describing the initial conditions for the particles is Eject-beam.f90

Looking at the fields

We start the postprocessor, and feed him with 
 -general
    infile= @last
 -3da
    symbol bla_e_5
    doit
The resulting plot is shown in figure 1.
Figure 1: The electric field at the fifth stored time. The coloured patches within the field are the macroparticles. The different colours of the macroparticles are because the macroparticles have different properties 'iColour'.
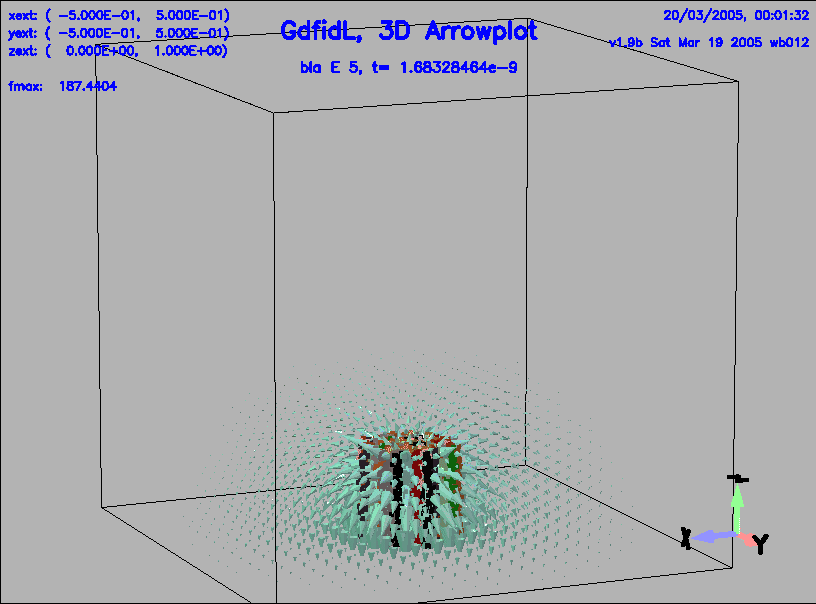\begin{figure}\centerline{ \psfig{figure=bla_e_5.PS,width=18cm,bbllx=0pt,bblly=0pt,bburx=745pt,bbury=553pt,clip=} }\end{figure}

Electron Gun, static voltages

Not yet written.

Photo Gun, initial fields, complicated current

We want to compute the motion of a small electron cloud which is created by a short laser pulse, and accelerated by a strong resonant field. The geometry is a rotational symmetric Photo Gun.

The requirements read: 

 Extract 1 nC of electrons from the cathode, located in the center
 of the cavity wall and having a 1 mm spot-size.
 The photoelectrons have a random distribution of longitudinal and
 transverse momentum with a total energy of 0.3 eV
 (mono-energetic for simplicity) and are extracted for 10 ps with a
 uniform time distribution (the transverse distribution is also
 uniform with cylindrical symmetry). The RF peak field on the cathode
 is 140 MV/m and the launching phase (beginning of the electron
 extraction) is 30 RF deg (90 deg is the max of the electric field).

The problem is the initial spot size of 1 mm. To be able to resolve such a small size charged cloud, one needs a gridspacing of 1/10 mm or less. As the size of the phot-gun is such that it fills a volume of about 10cm x 10cm x 10cm, a gridspacing of 1/10 mm would imply a grid with $10^9$ cells. Although it is possible to compute with such a large number of gridcells, we want to simulate at first with a more coarse grid, because computing with $10^9$ cells requires very much time and requires some tricks.

Photo Gun, coarse grid

We want to compute the motion of the charge as it is accelerated by a resonant field. We therefore have to know the resonant field, and use it as the initial condition for the time dependent field.

The inputfile for computing the resonant fields: Gun-coarse-resonant-fields.gdf We compute the resonant fields with the command 

 gd1 < Gun-coarse-resonant-fields.gdf | tee out-eigen

After some minutes, we get as list of frequencies: 

    i   freq(i)       acc(i)         cont(i)
    1    2.8525e+9   0.0000003154  0.0000002104       # "grep" for me
    2    2.8543e+9   0.0000000211  0.0000000239       # "grep" for me
    3    4.2757e+9   0.0000000488  0.0000000718       # "grep" for me
    4    4.2757e+9   0.0000000047  0.0000006255       # "grep" for me
    5    4.2918e+9   0.0000001127  0.0000149762       # "grep" for me
    6    4.2918e+9   0.0000000907  0.0000005142       # "grep" for me
    7    4.6768e+9   0.0000000056  0.0000000338       # "grep" for me
    8    4.6768e+9   0.0000000570  0.0000001797       # "grep" for me
    9    5.4438e+9   0.0000004153  0.0000015035       # "grep" for me
   10    5.7221e+9   0.0000006921  0.0000070810       # "grep" for me
   11    5.7373e+9   0.0000355960  0.0011519827       # "grep" for me
   12    5.8261e+9   0.0017362258  0.0569873187       # "grep" for me
   13    5.8445e+9   0.0006248663  0.0431812991       # "grep" for me
   14    5.8868e+9   0.0298497210  1.0000000000       # "grep" for me

There are two resonant fields with almost the same frequency of 2.85 GHz. Both are linear combinations of a 0-mode and a $\pi$-mode.

We look at the two first fields: 

 # Input for gd1.pp
 -gen, inf @last
 -3da, bbyhigh 0, sy e_1, do
 sy e_2, do
The resulting plots are shown in figures 2 and 3.
Figure 2: The electric field of the first resonant field.
\begin{figure}\centerline{ \psfig{figure=coarse-eigen-e_1.PS,width=18cm,bbllx=0pt,bblly=0pt,bburx=745pt,bbury=553pt,clip=} }\end{figure}
Figure 3: The electric field of the second resonant field.
\begin{figure}\centerline{ \psfig{figure=coarse-eigen-e_2.PS,width=18cm,bbllx=0pt,bblly=0pt,bburx=745pt,bbury=553pt,clip=} }\end{figure}
Instead of adjusting the geometry until a pure $\pi$-mode occurs, we take a proper linear combination of the two nearby modes and use that combination as the initial condition for the PIC computation.

Inspecting the z-component of the two resonant fields: 

 # Input for gd1.pp
 -gen, inf @last
 -lineplot
    sy e_1, do
    sy e_2, do
The resulting plots are shown in figures 4 and 5.

Figure 4: The Ez component of the first resonant field along the axis.
\begin{figure}\centerline{ \psfig{figure=coarse-eigen-ez_1.PS,width=18cm,bbllx=22pt,bblly=52pt,bburx=775pt,bbury=577pt,clip=} }\end{figure}

Figure 5: The Ez component of the second resonant field along the axis.
\begin{figure}\centerline{ \psfig{figure=coarse-eigen-ez_2.PS,width=18cm,bbllx=22pt,bblly=52pt,bburx=775pt,bbury=577pt,clip=} }\end{figure}

The Ez components of the two fields at the bottom of the cavity and in the center of the second cavity are 

 Ez(1,1)=  842, Ez(1,2)= 840
 Ez(2,1)= -849, Ez(2,2)= 427

The requirement on the accelerating field is, the peak value of the accelerating gradient near z=0 shall be 140 MV/m. The linearcombination of the two modes, which is a pi-mode, and which has a gradient of 140 MV/m at z=0, can be found from the solution of the linear equation: 

 a1 * Ez(1,1) + a2 * Ez(2,1) = 140e6
 a1 * Ez(2,1) + a2 * Ez(2,2) = 140e6

PIC-computation

For the PIC computation, we use the same geometry, and we use the proper linearcombination of the resonant fields as initial field. In the inputfile: 
 define(INFILE, /tmp/UserName/gun-eigen )

 #
 # Load the geometry from a previously computed case:
 # 
 -lgeometry
    infile= INFILE
    doit

The requirement on the accelerating field is, the peak value of the accelerating gradient near z=0 shall be 140 MV/m. The linearcombination of the two modes, which is a pi-mode, and which has a gradient of 140 MV/m at z=0, can be found from the solution of a linear equation. We can solve this system with GdfidL. In our inputfile, we solve for the amplitudes and specify that the resonant fields shall be loaded with that computed amplitudes: 

 define(G0, 140e6) # Wanted Gradient

 define(v11,  842) # Gradient of first field at z=0
 define(v12,  840) # Gradient of first field at z=p/2
 define(v21, -849) # Gradient of second field at z=0
 define(v22,  427) # Gradient of second field at z=p/2

 #
 # Solve the linear system.
 #
 define(a2, (G0-v12/v11*(-G0)) / (v22-v12/v11*v21) )
 define(a1, ( -G0 - v21*a2 ) / v11 )

 #
 # Load the initial field from a previously computed case
 # INFILE is a variable, which holds the name of the resultfile
 # of the resonant field computation.
 # 
 -linitialfields   
    infile= INFILE, symbol= e_1, static= no, factor= a1, doit
    infile= INFILE, symbol= e_2, static= no, factor= a2, doit

The full inputfile for performing the PIC computation: Gun-coarse-pic.gdf The sourcecode for the program describing the initial conditions for the particles is Eject-beam.f90 We start the computation with the command 

   gd1 < Gun-coarse-pic.gdf | tee out-pic

The computation takes only some minutes.

We then start the postprocessor: 

 # Input for gd1.pp
 -general, infile= @last
 ls
we get a list of datasets in the resultfile: 
 bla_h_1                Hds-3D time dependent t=   33.3769e-12
 bla_e_2                Eds-3D time dependent t=   66.7538e-12
 bla_h_2                Hds-3D time dependent t=   66.7538e-12
 bla_e_3                Eds-3D time dependent t=  100.1306e-12
 bla_h_3                Hds-3D time dependent t=  100.1306e-12
 bla_e_4                Eds-3D time dependent t=  133.5075e-12
 bla_h_4                Hds-3D time dependent t=  133.5075e-12
 bla_e_5                Eds-3D time dependent t=  166.8844e-12
 bla_h_5                Hds-3D time dependent t=  166.8844e-12
We have a look at the third, fourth and fifth stored electric field: 
 -3da, bbyhigh 0
   sy bla_e_3, do
   so 4, do
   so 5, do
The resulting plots are shown in figures 6, 7, 8.

Figure 6: The material boundaries of the cavity and the electric field. Only the material boundaries and the field below y=0 are shown. There are not yet any macroparticles in the volume.
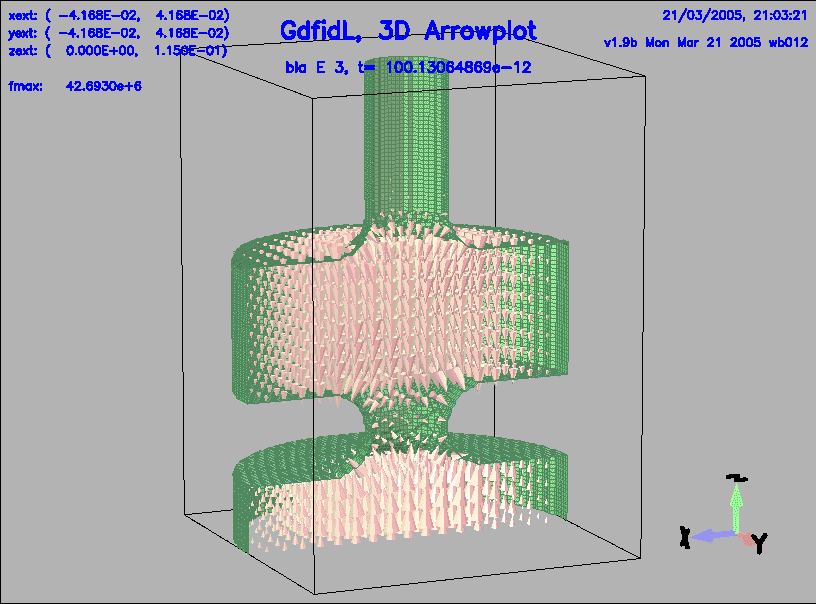\begin{figure}\centerline{ \psfig{figure=coarse-pic-e_3.PS,width=18cm,bbllx=0pt,bblly=0pt,bburx=746pt,bbury=553pt,clip=} }\end{figure}

Figure 7: The material boundaries of the cavity and the electric field. Only the material boundaries and the field below y=0 are shown. The coloured patches near the bottom of the cavity are the macroparticles. The macroparticles have just come into existence near the bottom of the cavity. Two species of particles were created. The particles of one species are accelerated into the cavity, the particles of the other species have been absorbed by the electric wall at the bottom of the cavity.
\begin{figure}\centerline{ \psfig{figure=coarse-pic-e_4.PS,width=18cm,bbllx=0pt,bblly=0pt,bburx=746pt,bbury=553pt,clip=} }\end{figure}

Figure 8: The material boundaries of the cavity and the electric field. Only the material boundaries and the field below y=0 are shown. The coloured patches near the bottom of the cavity are the macroparticles.
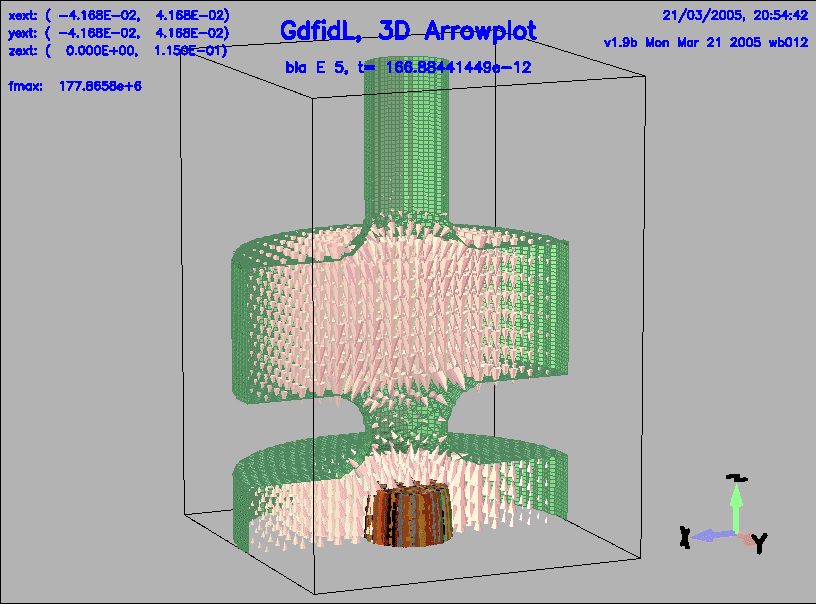\begin{figure}\centerline{ \psfig{figure=coarse-pic-e_5.PS,width=18cm,bbllx=0pt,bblly=0pt,bburx=746pt,bbury=553pt,clip=} }\end{figure}

Photo Gun, fine grid

Not yet written.


next_inactive up previous