Computations with free moving charges are done by GdfidL using the Particle in Cell algorithm (PIC). The PIC computation normally consists of three steps.
define(STPSZE, 1/100)
-mesh
spacing= STPSZE # The default grid spacing
pxlow= -1/2, pxhigh= 1/2 # The borderplanes of the computational volume
pylow= -1/2, pyhigh= 1/2 # pylow: Plane Y LOW
pzlow= 0, pzhigh= 1
cxlow= electric, cxhigh= electric # Condition at x=xlow, and at x=xhigh
cylow= electric, cyhigh= electric
czlow= electric, czhigh= electric
#
# Fill the 'universe' with vacuum:
#
-brick
material= 0
xlow= -INF, xhigh= INF
ylow= -INF, yhigh= INF
zlow= -INF, zhigh= INF
doit
-fdtd
-clouds
#
# We compile the executable file with the Fortran Compiler,
# (which is called 'fort' on this system)
#
system( fortran Eject-beam.f90 -o ./Eject-a.out )
#
# We specify that the properties of free moving charges
# shall be described by the executable file 'Eject-a.out'
#
ejectioncommand= Eject-a.out
In addition, we have to specify the time which shall be simulated.
And we should store some fields, to analyse the fields etc.
define(TMAX, 2/@clight)
-fdtd
-time
tmin= TMAX
tmax= TMAX
-storefieldsat
name= bla
what= both # 'what' could be 'e', 'b' or 'both'
# Clouds are stored anyway
firstsaved= 0.1 / @clight
lastsaved= 2 / @clight
distance= 0.1 / @clight
doit # do not forget this.
Now we can start the computation.
#
# Start of computation:
#
-fdtd
doit
The inputfile for this cavity is empty.gdf The sourcecode for the program describing the initial conditions for the particles is Eject-beam.f90
-general
infile= @last
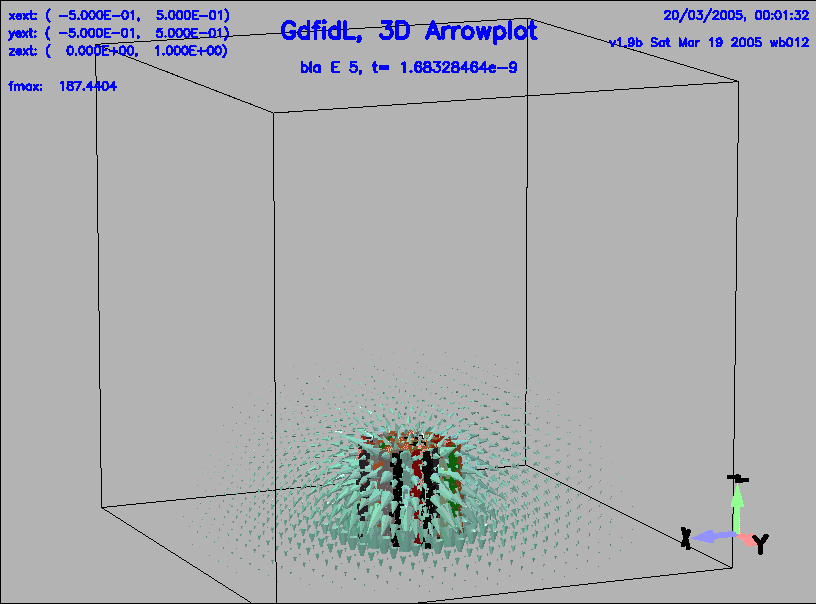
-3da
symbol bla_e_5
doit
The resulting plot is shown in figure 1.
 |
The requirements read:
Extract 1 nC of electrons from the cathode, located in the center of the cavity wall and having a 1 mm spot-size. The photoelectrons have a random distribution of longitudinal and transverse momentum with a total energy of 0.3 eV (mono-energetic for simplicity) and are extracted for 10 ps with a uniform time distribution (the transverse distribution is also uniform with cylindrical symmetry). The RF peak field on the cathode is 140 MV/m and the launching phase (beginning of the electron extraction) is 30 RF deg (90 deg is the max of the electric field).
The problem is the initial spot size of 1 mm.
To be able to resolve such a small size charged cloud, one needs a
gridspacing of 1/10 mm or less.
As the size of the phot-gun is such that it fills a volume of about
10cm x 10cm x 10cm, a gridspacing of 1/10 mm would imply a grid with
![]() cells. Although it is possible to compute with such a large number
of gridcells, we want to simulate at first with a more coarse grid,
because computing with
cells. Although it is possible to compute with such a large number
of gridcells, we want to simulate at first with a more coarse grid,
because computing with ![]() cells requires very much time and requires
some tricks.
cells requires very much time and requires
some tricks.
The inputfile for computing the resonant fields: Gun-coarse-resonant-fields.gdf We compute the resonant fields with the command
gd1 < Gun-coarse-resonant-fields.gdf | tee out-eigen
After some minutes, we get as list of frequencies:
i freq(i) acc(i) cont(i)
1 2.8525e+9 0.0000003154 0.0000002104 # "grep" for me
2 2.8543e+9 0.0000000211 0.0000000239 # "grep" for me
3 4.2757e+9 0.0000000488 0.0000000718 # "grep" for me
4 4.2757e+9 0.0000000047 0.0000006255 # "grep" for me
5 4.2918e+9 0.0000001127 0.0000149762 # "grep" for me
6 4.2918e+9 0.0000000907 0.0000005142 # "grep" for me
7 4.6768e+9 0.0000000056 0.0000000338 # "grep" for me
8 4.6768e+9 0.0000000570 0.0000001797 # "grep" for me
9 5.4438e+9 0.0000004153 0.0000015035 # "grep" for me
10 5.7221e+9 0.0000006921 0.0000070810 # "grep" for me
11 5.7373e+9 0.0000355960 0.0011519827 # "grep" for me
12 5.8261e+9 0.0017362258 0.0569873187 # "grep" for me
13 5.8445e+9 0.0006248663 0.0431812991 # "grep" for me
14 5.8868e+9 0.0298497210 1.0000000000 # "grep" for me
There are two resonant fields with almost the same
frequency of 2.85 GHz. Both are linear combinations of a 0-mode
and a ![]() -mode.
-mode.
We look at the two first fields:
# Input for gd1.pp -gen, inf @last -3da, bbyhigh 0, sy e_1, do sy e_2, doThe resulting plots are shown in figures 2 and 3. Instead of adjusting the geometry until a pure
Inspecting the z-component of the two resonant fields:
# Input for gd1.pp
-gen, inf @last
-lineplot
sy e_1, do
sy e_2, do
The resulting plots are shown in figures 4 and 5.
The Ez components of the two fields at the bottom of the cavity and in the center of the second cavity are
Ez(1,1)= 842, Ez(1,2)= 840 Ez(2,1)= -849, Ez(2,2)= 427
The requirement on the accelerating field is, the peak value of the accelerating gradient near z=0 shall be 140 MV/m. The linearcombination of the two modes, which is a pi-mode, and which has a gradient of 140 MV/m at z=0, can be found from the solution of the linear equation:
a1 * Ez(1,1) + a2 * Ez(2,1) = 140e6 a1 * Ez(2,1) + a2 * Ez(2,2) = 140e6
define(INFILE, /tmp/UserName/gun-eigen )
#
# Load the geometry from a previously computed case:
#
-lgeometry
infile= INFILE
doit
The requirement on the accelerating field is, the peak value of the accelerating gradient near z=0 shall be 140 MV/m. The linearcombination of the two modes, which is a pi-mode, and which has a gradient of 140 MV/m at z=0, can be found from the solution of a linear equation. We can solve this system with GdfidL. In our inputfile, we solve for the amplitudes and specify that the resonant fields shall be loaded with that computed amplitudes:
define(G0, 140e6) # Wanted Gradient
define(v11, 842) # Gradient of first field at z=0
define(v12, 840) # Gradient of first field at z=p/2
define(v21, -849) # Gradient of second field at z=0
define(v22, 427) # Gradient of second field at z=p/2
#
# Solve the linear system.
#
define(a2, (G0-v12/v11*(-G0)) / (v22-v12/v11*v21) )
define(a1, ( -G0 - v21*a2 ) / v11 )
#
# Load the initial field from a previously computed case
# INFILE is a variable, which holds the name of the resultfile
# of the resonant field computation.
#
-linitialfields
infile= INFILE, symbol= e_1, static= no, factor= a1, doit
infile= INFILE, symbol= e_2, static= no, factor= a2, doit
The full inputfile for performing the PIC computation: Gun-coarse-pic.gdf The sourcecode for the program describing the initial conditions for the particles is Eject-beam.f90 We start the computation with the command
gd1 < Gun-coarse-pic.gdf | tee out-pic
The computation takes only some minutes.
We then start the postprocessor:
# Input for gd1.pp -general, infile= @last lswe get a list of datasets in the resultfile:
bla_h_1 Hds-3D time dependent t= 33.3769e-12 bla_e_2 Eds-3D time dependent t= 66.7538e-12 bla_h_2 Hds-3D time dependent t= 66.7538e-12 bla_e_3 Eds-3D time dependent t= 100.1306e-12 bla_h_3 Hds-3D time dependent t= 100.1306e-12 bla_e_4 Eds-3D time dependent t= 133.5075e-12 bla_h_4 Hds-3D time dependent t= 133.5075e-12 bla_e_5 Eds-3D time dependent t= 166.8844e-12 bla_h_5 Hds-3D time dependent t= 166.8844e-12We have a look at the third, fourth and fifth stored electric field:
-3da, bbyhigh 0 sy bla_e_3, do so 4, do so 5, doThe resulting plots are shown in figures 6, 7, 8.
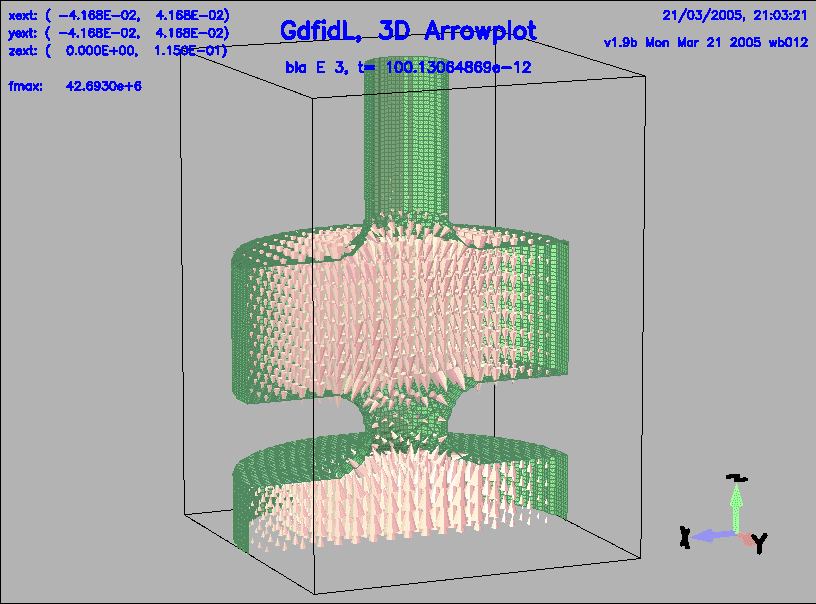 |
 |
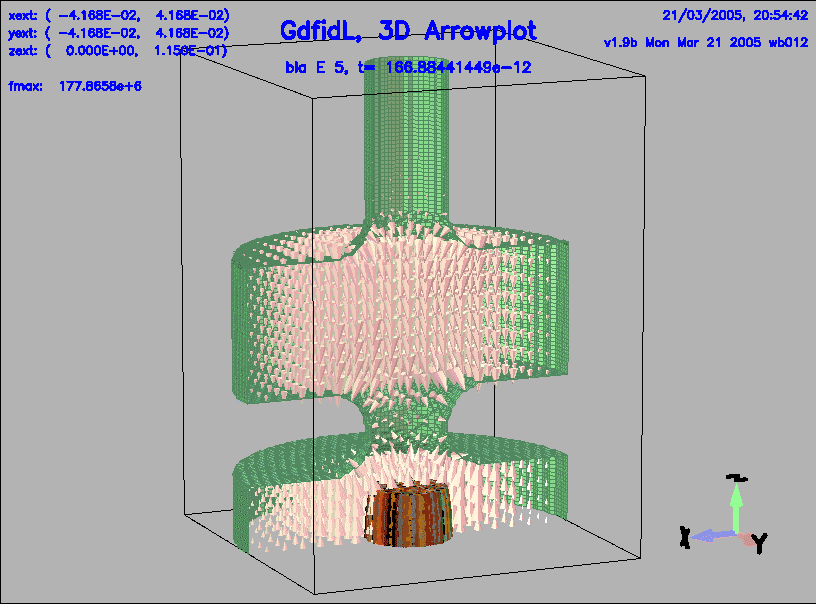 |